相対性理論は難しくない?のPart3です。今回は、「特殊相対性理論」の中の「空間の不思議」についてお話します。「空間」は過去から未来においてずっと変わらないものだと思っていませんか?実は「空間」も相対的に変わってしまうものなのです。

Part 2で、「時間は相対的なもので、静止している物に対して、動いている物の時間はゆっくり進む(時間が遅れる)」というお話をしました。
今回は、「空間」も相対的なものであり、一定ではない、「動いている物の長さは縮む」というお話です。
※「時間の遅れ」について詳しく知りたい方はこちら

動いている物が縮むなら、飛行機や電車も縮むのかな?
その通りです。ですが、その速度があまりにも遅いために、私たちが実感できるほど「縮む」ことはありません。
「光速に近い速度」で動くと、私たちが実感できるくらいに縮みます。

動くものは縮んで見える?


トンネルを例にしてお話します。車が猛スピードでトンネルの駆け抜けると、トンネルの長さは「縮む」のです。
動くものが縮むんでしょ? トンネルは動かないけど?


ですが、「相対的」には、車から見ると「トンネル」が動いているとも言えるのです。このことは読み進めていくと分かると思います。
まずは地上にいる人から見ると?
まずは、地上で静止している人から車を見るとどう見えるのか、ということからお話します。

秒速24万㎞(光速の80%)のスピードの車が、全長40万㎞のトンネルを走り抜けるとしましょう。どれくらいの時間でトンネルを抜けるでしょう?
40万㎞÷秒速24万㎞だから、だいたい1.67秒


「ふつう」ならそうなりますね。ですが、ここで問題なるのが「時間の遅れ」です。
動く物の時間は遅れて進む、ってやつね。

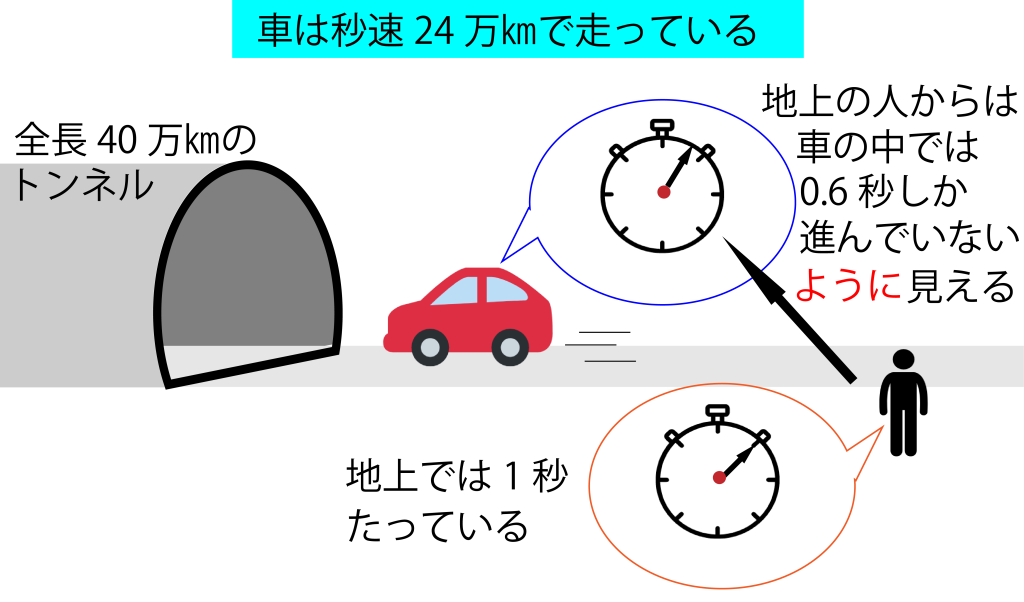
車は秒速24万㎞の猛スピードで動いているので、地上の人から見ると、地上で1秒進む間に、車の中では0.6秒しか進まないように見えます。
こうなると、トンネルを通過する時間は変わりますね。

(40万㎞÷秒速24万㎞)×0.6で、だいたい1秒かな。
そうです。「ふつう」なら、1.67秒かかるところですが、車の時間は「遅れる」ので、地上にいる人からは、車が1秒でトンネルを走り抜けたように見えます。

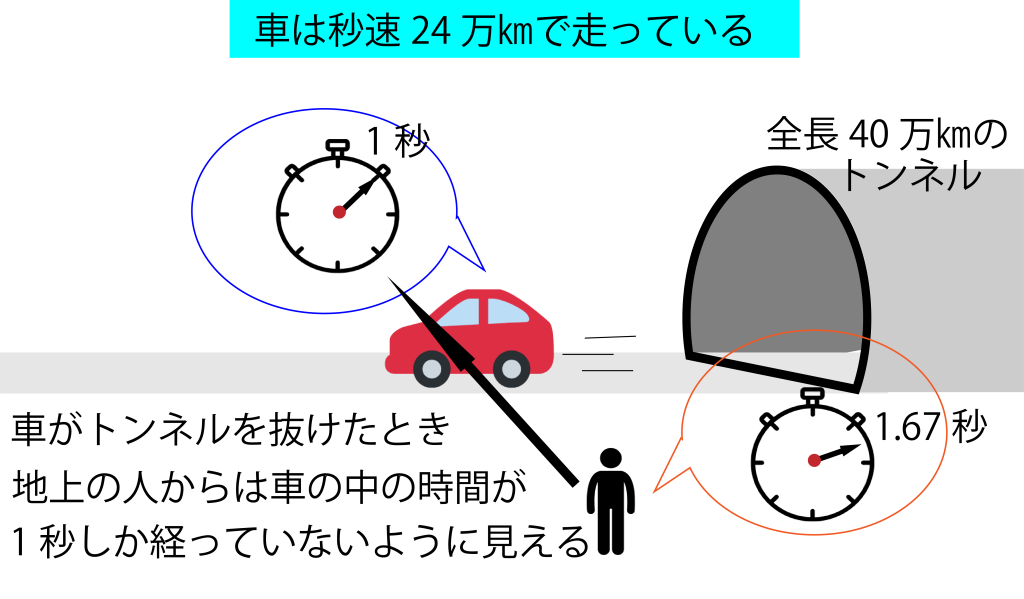
ここで、注意が必要なのは、「地上の人から車を見た場合」というところです。
上の図のように、地上のストップウォッチは1.67秒を刻みます。ですが、地上の人から、車の中のストップウォッチを見ると、1秒しか刻んでいないように見える、ということなんです。
では、「車の中の人」からはどう見えるのでしょうか?
車の中の人にはトンネルが縮んで見える?

ここで、注意が必要なのは、車の中の人にとっては、自分が静止していて、トンネルの方が動いていると考えても同じだ、ということです。
上の動画は、車がトンネルの中を走り抜けていますね。
でも、これを、「実は車は止まっていて、トンネルの方が動いている」と考えても、車はトンネルを抜けることができます。
「相対的」には、「車の方が動いていても」「トンネルの方が動いていても」同じだというわけです。

これで、「車の中の人」も、地上で静止している人と「立場」は同じになりますね。
なので、「車の中の人」にとっても、トンネルを1秒で抜けなければなりません。
なぜなら、動いているのはトンネルの方で、車の人は、静止しているからです。
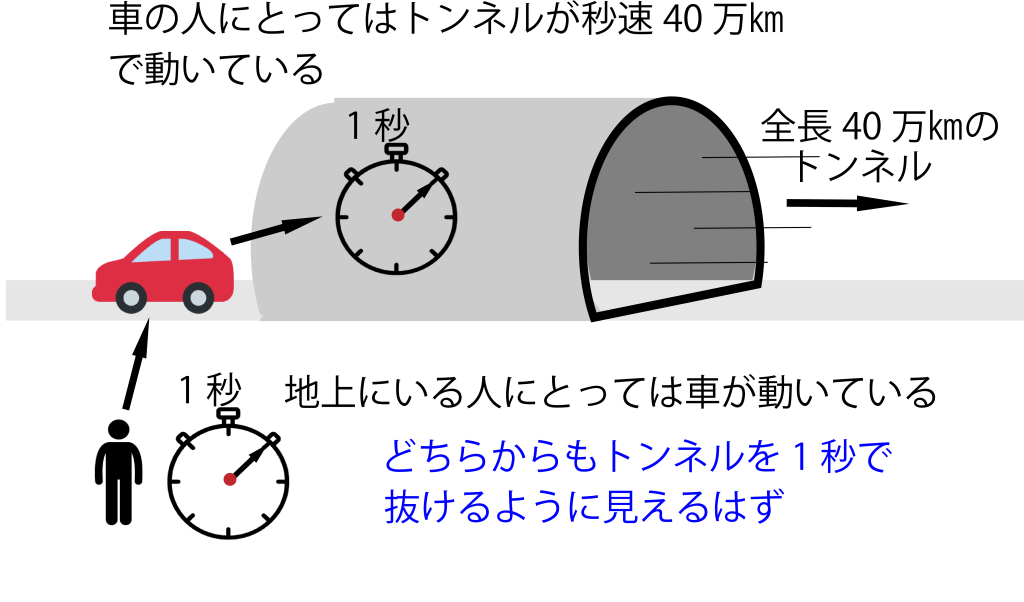
でも、40万㎞のトンネルが、秒速24万㎞で動いたなら、車がトンネルを抜けるのにやっぱり1.67秒かかるよね?


このままでは、そうなりますね。ではトンネルに何らかの変化が起こったらどうでしょう?
そっか!トンネルが縮めばいいのね!

そうです。トンネルは動いているので、縮みます。
ややこしい計算は省略しますが、長さ40万㎞のトンネルは、秒速24万㎞で動いているので、16万㎞も縮んで、24万㎞の長さになります。

24万㎞÷秒速24万㎞で1秒になるね!
このように、トンネルが縮むことで、静止している車から見ても、1秒でトンネルを抜けることになるのです。
はじめに言ったように、このようなことは、日常でも起こっています。ですが、日常レベルでは私たちが気づくまでの変化は起きません。
例えば、20mの長さのバスが、時速100㎞で走ってるとします。動いているので「バスは縮み」ますが、
この場合、86/1000000000000mm(1兆分の86mm)しか縮みません。
「動いているものは縮む」というのは事実ですが、光速に近いくらいの速さでなければ、はっきりとは分からないのです。
以上、お話してきたように、「相対性理論」によると、トンネルのような「空間」も、「時間」と同じように「相対的」に変化するものであり、「永遠に変わらないもの」ではないのです。
おしまい
Part4は、「質量とエネルギー」の話です。
興味のある方は是非!





コメント