なぜ月は地球に落ちてこないのか？天才ニュートンが考えた「万有引力の法則」について分かりやすく解説！

月は、なぜ地球に落ちてこないのか？ロケットはなぜ宇宙に行けるのか？それらの答えは、天才ニュートンの「万有引力の法則」にあります。今回は「万有引力の法則」について、小学生にも分かるように、やさしくお話します。

「万有引力」は誰でも聞いたことのある言葉ですよね。

そうです、有名なアイザック・ニュートンが、リンゴが木から落ちたのを見て、発見したと言われる「万有引力」です。

よく勘違かんちがいされるのが、ニュートンはリンゴが落ちるのを見て、「重力を発見した」。

だからすごい人なのだと。でも、そうではないのです。

リンゴが地面に落ちるのは、地球に「重力」があるからだ、ということは、ニュートンが登場する前から知られていました。

では、ニュートンが発見した「万有引力」とは、何がそんなにすごい発見なのでしょうか？

※ここでは、数式は出てきません。また難しい言葉にはルビがふってあります。

※ちなみに、ニュートンがリンゴが落ちるのを見て、「万有引力」を思いついた、というのは事実かどうかは、はっきりしないそうです。

「天動説」から「地動説」へ

ニュートンの話の前に、まず昔の科学者は宇宙をどう考えていたのかを簡単かんたんにご紹介しょうかいしていきます。

それを知ることで、ニュートンの「すごさ」がよりわかりますよ。

「天動説」とは？

天動説てんどうせつとは、「宇宙の中心は地球であり、太陽もその他の惑星わくせいも、すべて地球の周りをまわっている」という考え方です。

天動説を考えたのが、2世紀ころのプトレマイオスという科学者です。

今の人たちなら「そんなバカな」となりますが、この天動説は、その後1400年もの間、人々の間で信じられていたのです。

それはなぜでしょうか？

それは天動説でも、日常生活に何の不思議もないからです。

今では、地球は太陽の周りをものすごいスピードで公転していることは誰だれでも知っていますね。

（ちなみに公転のスピードは、時速1600キロほどです、音速よりも速いのです）

でもどうでしょう？　だからといって地球の外に放り出されることはありませんね。

また、朝、太陽が出てきて、どんどん空の上にあがり、沈みます。

どうでしょう？　これをいつも見ている人たちが、「太陽は地球の周りをまわっている」と考えても、何の不思議もないのです。

ですから、1400年もの長い間、人々は「地動説」を信じ続けたのです。

「天動説」から「地動説へ」

そして、16世紀。「いや地球が太陽の周りをまわっているのだ」という科学者が現れました。

この人も有名ですね。ガリレオ・ガリレイです。

ガリレオが登場する前にも、「地動説」と考えた科学者はいました。コペルニクスです。

ですが、コペルニクスは地球が太陽の周りをまわっているのだという「証拠しょうこ」を見つけることができませんでした。

その「証拠」を初めて見つけたのがガリレオでした。彼は当時には発明されていた望遠鏡ぼうんきょうで、月を見たのです。

ガリレオは驚おどろきました。

月の表面がデコボコしていたからです。

それまでは、宇宙にある星は「特別なもの」で、完全な球体きゅうたいだと思われていたからです。電球のように「つるっとしてキレイな球体」のように。

ですが、実際に見た月は、地球と同じようにデコボコしている、つまり「山」や「谷」がありました。

ガリレオは思いました、「月は特別な世界ではなく、地球と同じなのでは？」と。

このことが、「地動説」を信じるきっかけになりました。

次に、ガリレオは木星を観察かんさつしました。

そして、木星のまわりに小さな「点」がいくつかあるのを見つけました。

「点」は木星の衛星えいせいです。残念ながらこのころの望遠ぼうえん鏡きょうでは、木星の衛星えいせいは点にしか見えなかったのでしょう。

ちなみに、現在では木星の衛星えいせいは79個見つかっています。

その「点」を時間をかけて観察してみると「点」の数が減へることに気づきました。

ガリレオは不思議に思いました。

ですがこのことは、「点」が木星のまわりをまわっていて、時間によって木星にかくれて見えなくなってしまうのだ、と考えると理解できます。

　この時、ガリレオは考えました。「木星をまわる星があるのなら、地球が太陽のまわりをまわっていても、何の不思議もない」

くわしいことは、ここではお話しませんが、これをきっかけに、「天動説」ではありえない星の動きなどを、発見していきました。

「地動説」が正しいのだという「証拠しょうこ」次々に見つけていったのです。

しかし、ガリレイでも、人々に「地動説」を信じてもらうことはできませんでした。　

ガリレオは、地球や他の惑星わくせいが、どのようにして太陽の周りをまわっているのか、その惑星の「動き」をうまく説明することができなかったのです。

ケプラーの登場

その「惑星わくせいの動き」を説明したのが、ケプラーでした。

くわしく話すと難むずかしいので、ごく簡単かんたんにお話します。

ケプラーとガリレオの違ちがい。それは惑星わくせいが太陽をまわるときの「軌道きどう」の考え方でした。

「軌道」とは、上の写真の白い線です。惑星が太陽の周りをまわる「道」と考えてください。

赤い丸は「太陽」、青い丸は「地球」です。ケプラーは太陽をまわる地球の「軌道きどう」を楕円形だえんけいだと考えました。

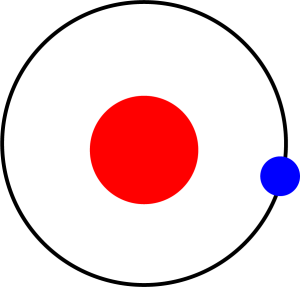
　ガリレオは「軌道」は完全でキレイな「円」だと考えていました。

　そのため、惑星の運動をうまく説明することが出来なかったのです。宇宙は「完全で美しい」ものだという考え方から抜ぬけ出すことが出来なかったのです

これは大変な発見でした。「軌道きどう」が楕円形だえんけいだとわかったケプラ―は、惑星の運動を予想して、それを「数式すうしき」にあてはめて、計算することで、惑星の運動を説明することに成功したのです。

「数式」。これが物理学ぶつりがくをキライになる原因だったりしますよね。私は高校生のころ物理学がキライでした。数式を計算することばかりだったからです。

ですから、ここではケプラーの「数式」は紹介しょうかいしません。「数式」を使わなくとも、科学者の「考え方」、または科学者が何を発見したかはわかるからです。

ですが、「数式」を使うことで、自分の考えたことを「証明しょうめい」する必要が科学者にはあります。簡単に言えば「数字はウソはつかないから」です。だから誰だれが見ても信用できる「証明しょうめい」になるのです。

話を戻もどしますね。

難むずしい話は抜ぬきにして、ケプラーは惑星の動きを正確に説明することに成功し、これをもって、1400年以上続いた「天動説」は終わりをむかえました。

彼は、惑星の運動のことで、3つの法則ほうそく（法則ほうそく＝「決まり事」と思ってください）を発見します。

ここでは、ニュートンに関係する、第2の法則だけご紹介しょうかいします。簡単かんたんに言いますと、

「太陽に近い惑星ほど、太陽の周りを速くまわっている」というものです。

なぜ太陽に近ければ公転こうてん（＝太陽の周りをまわること）するスピードが上がるのでしょうか？

ケプラーは、太陽と惑星の間に、何かの「力」が働いているからではないかと考えました。

それは磁石じしゃくが金属きんぞく（鉄など）を引きつける力のようなものではないかと考えましたが、その「力」の正体をつかむことはできませんでした。

その力の「正体」を突つき止めたのが、ニュートンだったのです。

ニュートンの登場

ここからは、ニュートンが発見したことは何か？についてお話していきます。

その正体は「引力」

初めにお話したように、リンゴが木から落ちる理由は、地球に重力があるからだ、ということはずいぶんと前からわかっていたことでした。

ですから、ニュートンがリンゴが落ちるの見ても、何も驚おどろくこともありませんでした。その理由はわかっていたからです。

では彼は、リンゴが落ちるのを見て、何を考えたのでしょうか？

すべての物体は、他の物体を引きつける「力」を持っているのではないか。そして、その「力」は地球の上だけではなく、宇宙にも当てはまるのではないか。

これがニュートンの大発見なのです。

リンゴが地球に落ちる理由も、惑星が太陽の周りをまわる理由もまったく同じなのでないかと考えたのです。

地球とリンゴはお互たがいを引っぱり合っている。太陽と地球も引っぱり合ってるし、地球と月も同じである。

これが宇宙で起こっている運動の「正体」だったのです。

前にもお話したように、ケプラーも、「太陽に近い惑星ほど速くまわっている」ということは、分かっていましたね。

でも、それが何の力によるものなのか、ということはわかりませんでした。

地球の上で起こることと、宇宙で起こることが同じだ、という考え方ができなかったからです。

どうしても、「宇宙では、地球上とは違う特別な力が働いているのではないか」という考え方から抜ぬけ出すことが出来なかったのです。

ですがニュートンは、宇宙は特別な場所ではなく、地球で起こることが、宇宙でも起きているだけなのだと考えたのです。

「天才」と言われている科学者たちが見つけることが出来なかった、力の「正体」を、ニュートンがついに見つけたのです。

ニュートンは発見したのは、次のことです。

「2つの物体の間には、引き合う力がある。そして、物体の質量しつりょうが大きければ大きいほど、その力は大きくなり、2つの物体の距きょ離りが近ければ近いほど、その力は大きくなる。そして、このことは、すべての物体が持つ力である」

ケプラーの「太陽に近い惑星が、より速くまわる」理由は、距離きょりが近ければ近いほど、その引力も大きくなるからなのです。

これが「万有引力」の法則です。「万有」とは「すべての物に有ある」ということです。

リンゴと地球で言えば、リンゴは地球に引っぱられいると同時に、リンゴも地球を引っぱっているのです。

ですが、リンゴの質量は、地球に比べると、とてつもなく小さいので、リンゴの方が、地球に引っぱられてしまいます。

だからリンゴは地球に落ちるのです。

このことは、もちろん地球と月、太陽と地球についても言えます。

月と地球はお互いに「引っぱり合って」います。

ですが、月の質量は地球に比べて小さいので、月は地球に「引っぱられて」しまいます。

また、あなたが友だちと一緒にいたなら、あなたと友だちは「引き合っています」。

だからといって、くっついたりしないですよね。それは人間の質量が、とてつもなく小さいため、2人の間に働く「引力」も、とてつもなく小さいからです。

ここで、問題が出てきます。月が地球に引っぱられているなら

「どうして月は地球に落ちてこないのでしょうか？」

「どうして月は地球の周りをすなおにまわっているのでしょうか？」

これには、ニュートンが発見した「万有引力」の法則ほうそくと、物体の運動を説明した3つの法則によって、答えることができます。

なぜ月は地球に落ちてこないのか？

地球と月は、おたがいに引っ張り合っています。

ですが地球の質量しつりょうの方が大きいので、月は地球に引っぱられます。

ではなぜ、月は地球に落ちてこないのでしょうか？

実は月は、地球に落ち続けているのです。

一体どういうことなのでしょう？

このことは、「万有引力の法則」と、第1の法則によって、説明することができます。

第1の法則とは簡単かんたんに言えばこういうことです。

「何の力も加えられなければ、止まっているものは、止まったまま、動いているものは、ずっと同じ方向に、おなじ速はやさで動き続ける」

これを「慣性かんせいの法則」と言います。

そして、この「止まっていよう」「動いていよう」とする力を「慣性力かんせいりょく」と言います。

赤い矢印やじるしは、地球の引力。黒い矢印は月が地球から離はなれていこうとする月の運動です。

宇宙では、月の運動を「止めよう」とする力はありません。ですから、慣性力かんせいりょくによって、地球から離はなれようとし続けます。

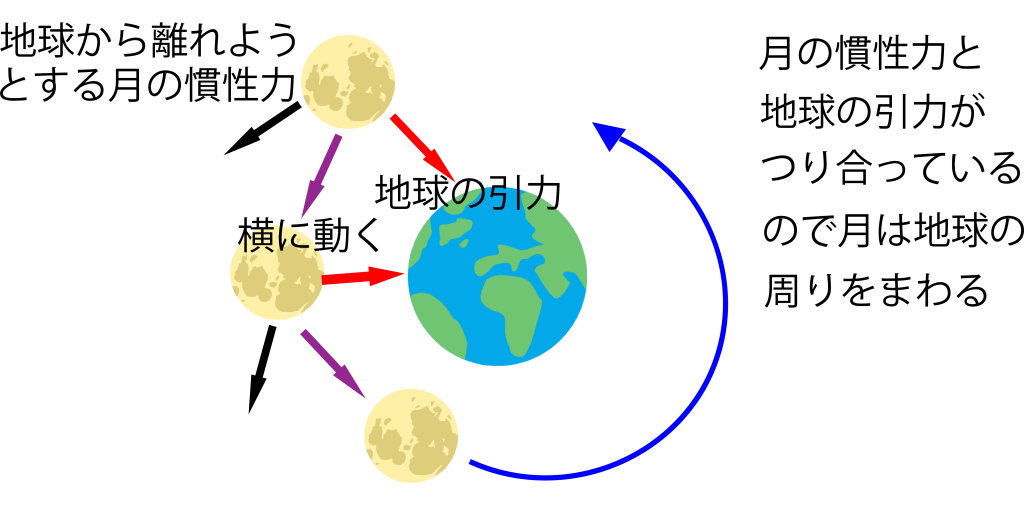
月は地球に引っ張られて、地球に落ち続けてはいますが（赤い矢印）同時に、地球から離はなれようと動き続けています（黒い矢印）

この2つの「力」が、ちょうどつりあっているので、地球に落ちることなく、ムラサキの矢印の方向に動きます。

このことを繰くり返して、月は「きちんと」地球の周りをまわることになるのです。

また、もし「離はなれろうとする力」のほうが強かったら、月は地球から離れ、宇宙のかなたへ飛んで行ってしまうでしょう。

次は「第2の法則」のお話しです。この法則は、物体の未来が「予測よそく」できる法則です。

物体の「未来」がわかる？

第2の法則はわかりにくいので、ごく簡単かんたんにお話しますね。

第2の法則は以下の通りです。

「物体に加くわえられる力が大きければ大きいほど、その物体の加速度かそくどは、大きくなる」

数式は使わない、と言いましたが、この数式は小学生にも理解できるものなので、ご紹介しょうかいします。

　F＝ｍ×a

Ｆ＝物体に加わる力　m=物体の質量　a=加速度　となります。

　※「加速度」とは、どんどんスピードが速くなっていくこと、と考えてください。

これ、そんなに難しいことではありません。例えば、こういうことです。

時速50㎞で走っている車があるとします。50㎞で走り続けたらなら、加速しないので「加速度」は0です。この車の質量は900㎏としましょう。

上の式に当てはめてみましょう。m=質量なので900、a=加速度なので、0　　Ｆ＝900×0　で、Ｆ＝0になります。

スピードが変わらない（加速度がない）ので、加えられた力は「0」となります。

次に、止まっている車に力を加えて、加速させるとしましょう。その力Ｆ（加えられた力）が900としましょう。

力が加えられたので、今度は加速度は0ではないので、どんどん加速していきます。

では式にあてはめます。

　900＝900×a となりますね。a（加速度）は「1」となります。

加速度1の車は、1秒ごとに速度が1m/sずつ増えていきます。（m/sとは秒速1mのことです）

加速度10なら1秒ごとに速度が10m/sずつ増えていく、ということです。

では、これが一体何なのか、ということですが、深く説明するとややこしくなるので、こう考えてください。

「物体の運動を計算することで、その物体がどのような運動をするのか正確にわかる」

その物体が、2時間後・10時間後に「どこにいるのか」が正確にわかる、ということです。

例では「車」でしたが、もちろんこれは、地球などの惑星にもあてはまります。

つまり、この法則によって、惑星などの運動が正確に「予測よそく」出来るようになったのです。

これが、物体の「未来」がわかる、ということなのです。

次は最後の第3の法則についてお話します。

この法則があるからロケットは宇宙に行けるのですよ。

ロケットが宇宙に行けるのはなぜ？

第3の法則を簡単に言うと次の通りです。

「物を押したら、同じ大きさの力で、反対方向に押し返される」

あなたがカベを、思いっ切り押したとしましょう。

その時、後ろに押し返されますね。これを「作用さよう・反作用はんさようの法則」と言います。

ロケットが、宇宙に向かって飛んでいくのも、この「作用・反作用の法則」があるからです。

ロケットは、ジェット噴射ふんしゃによって、ものすごい「力」で地球を押します。

するとこの「力」と同じ大きさの「力」が反対にロケットを押します。

そして、ロケットは宇宙へと向けて、空に上がっていくのです。

例えば、こんなことも言えます。みなさんは暗いとき、懐中電かいちゅうでん灯とうを前に向けますね。

この時、懐中電灯かいちゅうでんとうからは、「光のエネルギー」が出ています。エネルギーとは「力」です。前に向けて「力」を出しています。

「作用・反作用の法則」によると、反対方向にも同じだけの「力」が働くので、この時、懐中電灯を持っている手が、押されているはずです。

でも懐中電灯を使っていて、後ろに手が押されたことはありませんよね。

これは、その「力」があまりにも小さいために、「感じない」だけで、手はちゃんと後ろに「押されて」いるのです。

おわりに

以上、ニュートンの大発見について、お話してきました。

もう一度言いますが、「万有引力」を発見したから、ニュートンはすごいのではありません。

地球で起こっていることは、宇宙でも起こっているのだと考えたところが、すごい「発想はそう」であり、「大発見」だったのです。

それまでは、宇宙とは「神様が作った特別な場所」でした。

ですが、ニュートンは、そんな「特別な場所」はないと考えたのです。

そして、この考え方は、その後の宇宙をガラリと変えることになりました。

1人の天才が、それまでの「常識じょうしき」をひっくり返したのです。

先にも言いましたが、ぼくは高校の時、物理学ぶつりがくがキライでした。ひたすら、数式すうしきとにらめっこの授業じゅぎょうだったからです。

でも、物理学とは、この世の中の「仕組み」を解とき明あかす学問です。決して数式すうしきを解とくだけの学問ではありません。

それがわかった時、ぼくは物理学が好きになり、それからたくさんの物理の本を読みました。もちろん数式があまり書かれていない本を。

今回のお話を読んで、少しでも「物理学ぶつりがく」がおもしろいと思っていただけたら、幸いです。

おしまい